Dans la série des objets mathématiques fascinants (voir "Art et mathématiques"),
les fractales occupent une belle place !

Les deux propriétés particulières d'une fractale:
elle est issue d'un processus itératif ou récursif (processus en boucle, répété indéfiniment dans lequel le résultat obtenu à une étape du processus est réinjecté dans l'étape suivante).
elle présente un caractère d'auto-similarité (toutes ses parties, jusqu'à la plus petite, ressemblent au tout, et inversement).

	Récursivité. Un chapitre de "Intuition, intention, programmation": fractales et processus en boucles. Télécharger (PDF - 1,1 Mo).
	Intuition, intention, programmation. Une introduction à la programmation pour les étudiant(e)s en arts numériques, en préambule à l’utilisation du logiciel PROCESSING. Télécharger ici le document entier (PDF - 15,8 Mo).

On obtient une image fractale en partant d’un objet graphique
auquel on applique une certaine transformation qui ajoute un élément de complexité,
puis en appliquant la même transformation au nouvel objet ainsi obtenu,
ce qui accroît encore sa complexité... et en recommençant à l’infini ce processus d’itération.

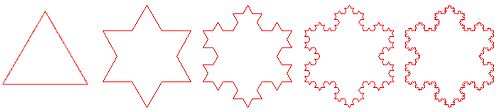
Un exemple classique de fractale, la courbe de von Koch, appelée également
"flocon de neige de von Koch". Cette courbe s’obtient en appliquant à chaque côté d’un triangle
équilatéral une transformation simple : on remplace le 1/3 central de chaque côté par 2 segments
ayant la même longueur que celle qui a été prélevée et on recommence la même opération sur chaque
côté de la figure obtenue.

À la première itération ("Action de répéter, de faire de nouveau" Petit Larousse), on obtient une image
proche d’une étoile de David, puis au fur et à mesure des itérations successives le résultat mime
plus ou moins un flocon de neige.



Remarquons au passage qu’il est matériellement impossible de dessiner exactement une fractale
puisqu’il faudrait poursuivre les itérations à l’infini.
En pratique on s’arrête quand les plus petits détails sont inférieurs à la résolution de l’écran.

Ce type de courbe présente une particularité bien curieuse. La première intuition conduit à penser que le périmètre de cette figure tend vers une valeur limite finie, puisqu’on ajoute des détails de plus en plus petits au fur et à mesure des itérations successives. En réalité, à la première itération la longueur L de chaque côté est remplacée par 4 segments de longueur L/3 ; à la deuxième elle devient 16 L/9... À chaque itération la longueur est donc multipliée par 4/3, ce qui signifie que (contrairement à l’intuition première) la longueur d’une courbe de Koch tend vers l’infini pour un nombre d’itérations infini (série géométrique de raison 4/3). Et pourtant cette courbe ne déborde à aucun moment des limites constituées à l’extérieur par le cercle circonscrit au triangle initial, et à l’intérieur par le cercle inscrit dans ce triangle ! En d’autres termes une surface de dimension finie est limitée par une frontière de longueur infinie.


Charles Vassalo. Art et fractales.
The Chaos Hypertextbook. Mathematics in the Age of the Computer, par Glenn Elert.
Mathematical Art. Graphics, Chaos and Fractals.
Fractal expressionism. Un chapitre de The Mechanics of Expression, un cours de Remko Scha.

Marie-France et de Jean-Paul Hellot.
Nick Steven's Frax 4D Fractals.
Fractal Buddha. Fractales et théorie du chaos.
The Self-Similar Cosmological model.
Fractal Cosmology.
Mandelbrot Cosmology.
M-Set as metaphor.
Astronomy Picture of the Day Archive.
What are Fractals ?
What are Fractals ? Par le Jim Tucek, un garçon assez grincheux.

Snow crystals. Cristaux et autres phénomènes dûs au gel.
Wilson A. Bentley. The Snowflake Man... Photographe et passionné de cristaux de neige.
Observations of Snow Cover from the Ground and Space.